Given figure, AY⊥ ZY and BY ⊥ XY, such that AY = ZY and BY = XY. Prove that AB=ZX

CBSE Class 9 CBSE Class 9 Maths
1

In the given figure, AY⊥ ZY and BY ⊥ XY, such that AY = ZY and BY = XY. Prove that AB=ZX
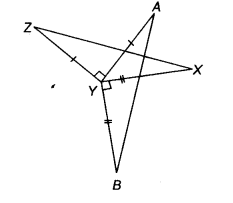
image

2

Given AY = ZY ; AY⊥ZY
and BY = XY;BY⊥XY
To prove AB = ZX
Proof ∵BY⊥ XY and AY ⊥ ZY
∴∠BYX = 90°
and ∠AYZ = 90°
=>∴BYX =∴AYZ
On adding∠AYX both sides, we get
∠BYX+ ∠AYX =∠AYZ + ∠AYX
=> ∠AYB = ∠ZYX
Now, in ∆AYB and ∆ZYX, we have
AY = ZY
BY = XY
and ∠AYB = ∠ZYX [proved above]
image
[by SAS congruence rule]
AB = ZX