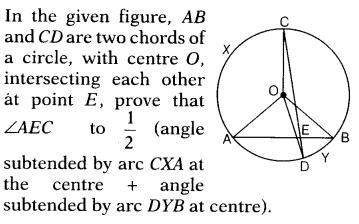
Given AB and CD are two chords of circle with centre O, which intersects at E.
![]()
Construction Join AC, BC and BD.
Proof AC is a chord.
∴ ∠AOC=2∠ABC…(i)
[angle subtended at centre is double the angle subtended at circumference]
Similarly, ∠DOB = 2DCB… (ii)
[angle subtended by the chord BD]
On adding Eqs. (i) and (ii),
we get ∠AOC + ∠DOB = 2(∠ABC + ∠DCB) …(iii)
In ∆CEB,∠AEC = ∠ECB + ∠CBE
[exterior angle is equal to the sum of two opposite interior angles ]
∠AEC = ∠DCB +∠ABC ,…(iv)
[∴ ∠ECB =∠DCB and ∠CBE ∠ABC] :.
From Eqs. (iii) and (iv), we get
∠AOC + ∠DOB =2∠AEC