In the given figure, ABCD, DCFE and ABFE are parallelograms. Show that ar (∆ADE) = ar (∆BCF).
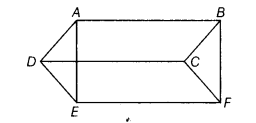
Given ABCD, DCFE and ABFE are parallelograms.
To prove ar (∆ADE) = ar (∆BCF)
Proof Since, ABCD is a parallelogram.
∴AD = BC …(i)
[∵ opposite sides of a parallelogram are equal]
Similarly, as DCFE and ABFE are parallelograms.
∴ DE = CF and AE = BF …(ii)
[∵ opposite sides of a parallelogram are equal]
Thus, in ∆ADE and ∆BCF, we have
AD = BC [from Eq. (i)]
DE=CF [from Eq. (ii)]
and AE = BF [from Eq. (ii)]
∴∆ADE = ∆BCF
[by SSS congruence criterion] => ar(∆ADE) = ar(∆BCP)
[∵ congruent figures have equal areas]