Find the voltage ?V1 across the first capacitor.
Express your answer in terms of V ?
Find the charge Q on the first capacitor.
Express your answer in terms of C and ?V1.
Using the value of Q just calculated, find the equivalent capacitance Ceq for this combination of capacitors in series.
Express your answer in terms of C.
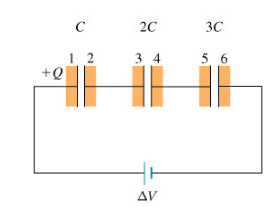
Concepts and reason
The concept which is used to solve the problem is capacitance of the parallel plate capacitor.
First, calculate the voltage across the capacitor 1, 2, and 3 by using capacitance formula. Add the voltages across 1, 2, and 3 to calculate the voltage across the first capacitor in terms of V. Next, calculate the charge on first capacitor by using capacitance formula. Finally, calculate the equivalent capacitance by using the relation between capacitance and the voltage.
Fundamentals
Capacitance of the capacitor is the ratio of charge and voltage.
Expression for voltage across the capacitor is,
![]()
Here, Q is the charge and V is the voltage.
Answer:
Expression for voltage across the capacitor is,
![]()
Here, Q is the charge and V is the voltage.
Rearrange the above equation for V.
![]()
The expression for the voltage across the first capacitor is,
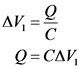
The expression for the voltage across the second capacitor is,
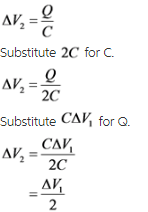
The expression for the voltage across the third capacitor is,

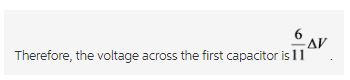
Explanation:
If a voltage applied to the plates of the capacitor, an electrical current flows charging up one plate with a positive charge with respect to the supply voltage and the other plate with an equal and opposite negative charge.
Expression for the charge on capacitor is,

Explanation:
Capacitance of a capacitor is the ability of capacitor to store an electric charge. Voltage is the amount of potential energy between the two points in a circuit.
The equivalent capacitance in series is,
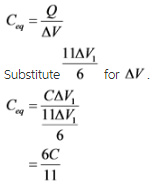

Explanation:
If two capacitors are connected in series, then the charge on the capacitor remains constant. If the two capacitors are connected in parallel, then the voltage remains constant.
The equivalent capacitance of the capacitors in series is,
![]()