Find out electric field intensity due to a uniformly charged infinite plane sheet?
Let’s consider a thin, infinite plane sheet of charge with uniform surface charge density
cm-2.
From the understanding of symmetry principles, it can be stated that the electric field lines will emanate normally from this surface.
Let us calculate electric field due to this sheet.
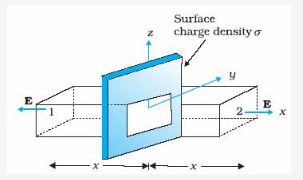
The suitable Gaussian surface would be a rectangular parallelepiped of cross sectional area A. It is clearly visible from above fig that, only the two faces1 and 2 will contribute to the flux (the unit vector 
is and
are parallel to each other). The electric field lines are perpendicular to the other faces and therefore, do not contribute to the total flux.
Therefore electric flux over these edges 
are equal and add up (As the unit vector to surface 1 is in –x direction while for surface 2, it is in +x direction).
That is net flux through the Gaussian surface=2 EA
But, the net charge enclosed by the closed surface, q = x A
where 
is the unit vector in the direction of the outward normal to the sheet of charge.
The nature of charge distribution decides the direction of electric field vector.
If 
>0 , the direction of is directed outwards.
If <0 , the direction of is directed inwards.
It is clear from the above expression that E is independent of the distance of the point from the plane charged sheet.