Figure shows an equiconvex lens (of refractive index 1.50) BL in contact with a liquid layer on top of a plane mirror. A small needle with its tip on the principal axis is moved along the axis until its inverted image is found at the position of the needle. The distance of the needle from the lens is measured to be 45.0 cm.
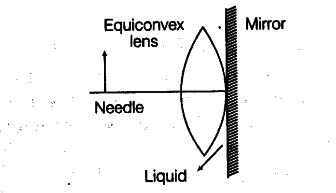
The liquid is removed and the experiment is repeated. The new distance is measured to be 30.0 cm. What is the refractive index of the liquid?
If f_{ 1 } is focal length of double convex lens of glass, then f_{ 1 } = 30 cm
Focal length of combination of double convex lens and plano-concave liquid lens,
f = 45 cm. .
Refractive index of lens,
µ_{ g } = 1.5
Let f_{ 2 } be the focal length of the plano-concave lens made of liquid between the convex lens and plane mirror.
For combination of lenses,
1/f_{ 1 } + 1/f_{ 2 } = 1/f
1/30 + 1/f_{ 2 } = 1/45
1/f_{ 2 } = 1/45 - 1/30 = -1/90
f_{ 2 } = -90 cm
We know that radii of curvature of two surfaces of plano-concave lens of liquid formed between foci of convex lens and plane mirror are -R and ∞
For the convex lens of glass,
R _{ 1 } = R
R_{ 2 } = -R
Using lens maker’s formula,

