Expression of center of mass of a two-particle system in easy way
The centre of mass is an imaginary point where one can assume the entire mass of the given system or object to be positioned.
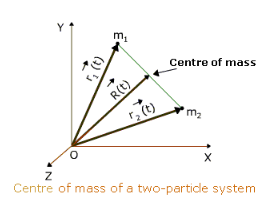
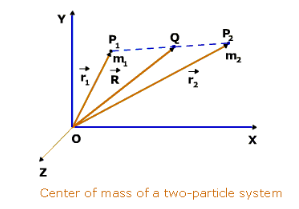
Consider a system consisting of two point masses m1 and m2, whose position vectors at a time t with reference to the origin O of the inertial frame are
respectively.
This can be written mathematically as
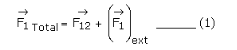
Similarly, for the point mass m2 ,
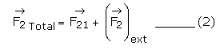
According to the Newton’s second law of motion, the equation of motion of point mass m1 is
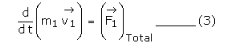
Similarly, for the second particle
Adding equations (3) and (4), we get
which implies,
From (1) and (2),
According to Newton’s third law,
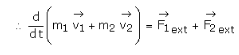
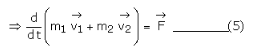
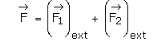
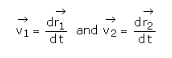
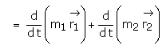
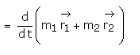
From equation (5),
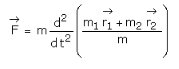
Where m = m1 + m2, that is the mass of a hypothetical object. Its position at any time is given by position vector such that,
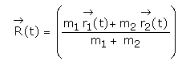
This is nothing but the position vector
and is called the centre of the mass of the two-particle system.
It is the point where the total external force
is supposed to act.
For a two-particle system, the centre of mass lies between the two particles and on the line joining them.
If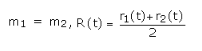 
i.e., the mid-point of the line joining the masses.