Explain the polygon law of vector addition?
Polygon law of vector addition states that if a number of vectors can be represented in magnitude and direction by the sides of a polygon taken in the same order, then their resultant is represented in magnitude and direction by the closing side of the polygon taken in the opposite order.
Let us find the resultant of four vectors 
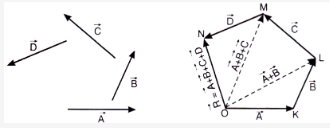
In traingle OKL, the vectors 
are represented by the sides taken in the same order. Therefore, from the triangle law of vector addition, the closing side taken in the opposite order represents the resultant of vectors .
Thus, 
. … (1)
By applying the traingle law of vector addition to the traingle OLM, It shows that the side 
is the resultant of vectors i.e., .
Using eg (1), we get,
… (2)
Similarly applying the triangle law of vector addition to the triangle OMN, we get,
Using eq (2), we get,
… (3)
Now the vectors 
.
Denoting the vector, 
, the equation becomes,
