Explain clearly with examples, the distinction between
(i) magnitude of displacement (sometimes called distance) over an interval of time and the total length of the path covered by a particle over the same interval.
(ii) magnitude of average velocity over an interval of time and the average speed over the same interval. [Average speed of a particle over an interval of time is defined as the total path length divided by the time interval]. Show in both (a) and (b) that the second quantity is either greater than or equal to first. When is the
’ equality sign true? [For simplicity, consider one-dimensional motion only]
(i) Magnitude of displacement of a particle in motion for a given .time is the shortest distance between the total length of the path covered by particle is the length of actual path traversed by the particle in the given time.
(ii) Let us consider an example
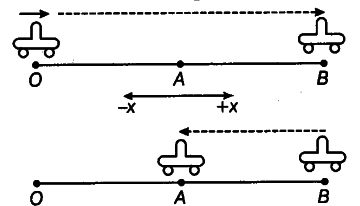
A car starts from O and moves along positive x-axis. The car stops "at B and starts moving towards negative x-axis. Finally, the car reaches at A.
For the motion from O to B,
So, |Displacement| = Distance covered
|Average velocityl = Average speed
For the motion from O—>B—>A So, | Displacement| < Distance covered
|Average velocity| < Average speed