Explain clearly, with examples, the distinction between:
(a) Magnitude of displacement (sometimes called distance) over an interval of time and the total length of path covered by a particle over the same interval.
(b) Magnitude of average velocity over an interval of time and the average speed over the same interval. [Average speed of a particle over an interval of time is defined as the total path length divided by the time interval]. Show in both (a) and (b) that the second quantity is either greater than or equal to the first When is the equality sign true ? [For simplicity, consider one dimensional motion only
(a) Magnitude of displacement or distance covered by a body in a given time interval is the difference between the initial and final positions of the body. It can be expresse
The total length of a body travelled by the length of the actual path covered by it. The total length of the path is either equal or greater than the magnitude of the displacement.
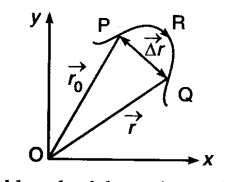
(b) Suppose a particle at times t1 and t2 be at the positions P and Q, respectively
.’. Average velocity between t1 and t2
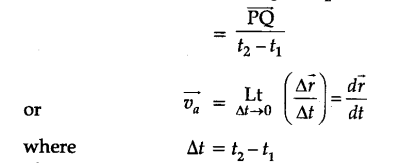
The average velocity does represent us whether the motion of the particle was actually along the path PQ or along PRQ and whether the motion between t1and f2 was steady or not. Average speed is defined as the ratio of the total distance covered by the body to the toted time taken. E.g., suppose a person goes to a temple 1 km away from his house and comes back taking 1 hour to perform the journey both ways.
Average speed of the man = 1+1/1=2km/h
But average velocity is zero because his displacement during the time of 1 hour is zero.
So, in either case (a) and (b) the second quantity is either greater them or equal to the first quantity. Equality sign is correct when displacement is equal to the distance. It holds when body moves along a straight path