The sap in trees, which consists mainly of water in summer, rises in a system of capillaries of radius r = 2.5 x ${{10}^{-5}}$m. The surface tension of sap is 5 = 7.28 x ${{10}^{-2}}$ N/m and angle of contact is 0°. Does surface tension alone account for the supply of water to the top of all trees?
Given, radius ® = 2.5 x${{10}^{-5}}m
Surface tension (5) = 7.28 X {{10}^{-2}} N/m
Angle of contact (θ) = 0°, density of water (p) ={{10}^{3}} kg/{{m}^{3}}$
The maximum height to which sap can rise in trees through capillarity action is given by
h = 2S cos θ / r ρg
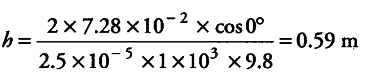
But the height of many trees are more than 0.59 m, therefore, the rise of sap in all trees is not possible through capillarity action alone.