Describe parallax method for measuring large distances.
Parallax is a method of measuring distance to an object. Similar to how our binocular vision helps us determine distance, the direction to a distant point is slightly different from two separate observation positions. If the distance between the observation positions is known, and the angle between them can be measured, it is a matter of simple geometry to calculate the distance to the object. It is a relatively simple concept but is one of the most important for making astronomical observations.
In astronomy, the parallax method is a means of measuring the distance between our solar system and a star up to 1600 light years away. This method is not limited to astronomy; it can in fact be applied to any physically similar situation. Before radar-mapping by satellite, the parallax of a mountaintop relative to the horizon was used by surveyors to determine its elevation when the distance to the summit was known.
Determination of distance of moon from earth (by parallax method)
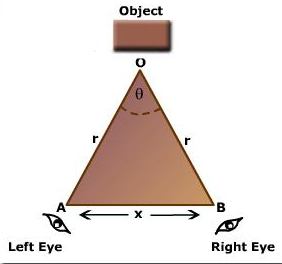
Let the object O be viewed with our eyes which is at a distance of r, making an angle q between the two eyes as shown in the diagram.
The angle q, caused by the two lines drawn from the position of the two eyes to the object, is called angle of parallax.
If we can consider OA and OB as radius of a circle and the distance x (AB) as arc of the circle, then we have
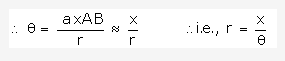
By knowing the values of x and q, the distance of the object from the point of observation can be found out.
However, if we consider O, referred in the above diagram to be the moon or a nearby star, then the angle q is too small in the view of the large astronomical distance and the place of observation. Hence, in order to have a better and valid point of observation, two points on the surface of the Earth is taken as the basis for observation instead of the two eyes. In order to have simultaneous observation of the moon, we select a very distant star at O and measure the angle between O and the two points on the Earth, as shown in the diagram below
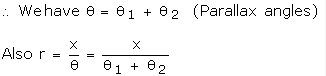
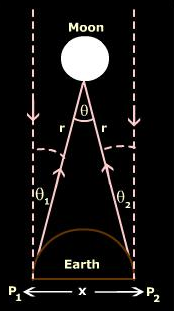
Thus, the distance of the moon or a distant star from the Earth can be found out.