Derive the expression for electric field intensity due to a uniformly charged thin spherical shell.
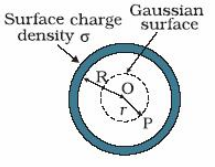
Let
the uniform surface charge density of a thin spherical shell of radius R .Let us find out electric field intensity at a point P outside or inside the shell.
-
Field outside the shell-
Let us find out electric field intensity at a point P outside the spherical shell, such that OP=r. Here we take Gaussian surface as a sphere of radius r. the electric field intensity,
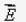
is same at every point of Gaussian surface, directed radially outwards (as is unit vector
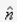
, so that
)
Hence it is clear that electric intensity at any point outside the spherical shell is such, as if the entire charge is concentrated at the centre of the shell. -
Field at the surface of the shell-
For this we have r = R
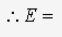
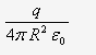
If
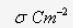
is the charge density on the shell, then
-
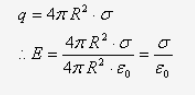
Field inside the shell -
If the point P lies inside the spherical shell, then Gaussian surface is a surface of sphere of radius r
As there is no charge inside the spherical shell, Gaussian surface encloses no charge.
That is q=0
Hence the field inside the spherical shell is always zero.
E = 0
Hence the field inside the spherical shell is always zero.