Derive coulombs law in vector form_______

[Dhanalakshmi]

Derive coulombs law in vector form_______.

[Dhanalakshmi]

Coulomb measured the force between two point charges and found that it varied inversly as the square of the distance between the charges and was directly proportional to the product of the magnitude of two charges and acted along the line of joining the two charges.
Thus if two point charges q₁ and q₂ are separated by a distance r in vacuum,
the magnitude of the force F between them is given by,
…(1)

The constant k in eqn.(1) is usually put as, so that Coulombs law is written as

…(2)

where εo is permitivity of free space and it is given by, εo = 8.854×10^-12 C²N^-1m^-2
Since force is vector, we need to write Coulombs law in vector notation.

vector quantity is given in Bold)

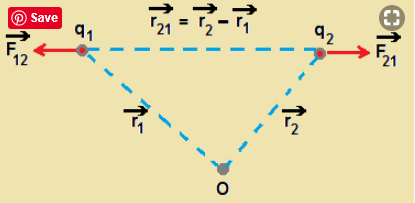
Let the position vectors of charges q₁ and q₂ be r₁ and r₂ respectively. We denote force on q₁ due to q₂ by F₁₂ and

force on q₂ by q₁ by F₂₁ as shown in figure. The two point charges q₁ and q₂ have been numbered 1 and 2 for conveneience

and the vector leading from 1 to 2 is denoted by r₂₁

r₂₁ = r₂-r₁ . The magnitude of vector r₂₁ is denoted by | r₂₁ |. The direction of a vector is specified by unit vector along that vector.

We define the unit vector

Coulombs force law between two point charges q₁ and q₂ located at r₁ and r₂ is then expressed as

The above equation is valid for any sign of q₁ and q₂. If q₁ and q₂ are of same sign, F₂₁ is along r₂₁ , which denotes repulsion.

If they are opposite sign, F₂₁ is along -r₂₁ that denotes attraction. No need to write separate equation for like and unlike charges