derive an mathematical expression for centripetal force with full explanation in lucid language
Let us consider a particle of mass ‘m’ be moving in a circle of radius ‘r’ with a constant speed ‘v’. Consider that the point is at A at any instant and then at B after a short time ‘t’.
Thus, AB = vt
The velocity at A is along the tangent AL and at B is along the tangent BM, i.e., the two vectors AL and BM represent the veolcity at A and B respectively and are equal in length (since speed is the same, v)
Draw O’a parallel to and equal to vector AL which represents the velocity ‘v’ at A. Similarly, draw O’b parallel to and equal to vector BM which represents the velocity ‘v’ at B, a short time t later.
O’a = O’b = v.
From the law of triangle of velocities, ab represents the change in velocity.
Rate of change of velocity, i.e. acceleration acting on the particle is given as the change in velocity ab taken place in time t, i.e. ab/t.
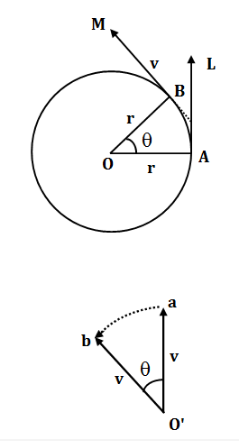
When the time t is very short, AB is almost a straight line and AOB is a ΔAOB and ΔO’ab are similar.
