Derive an expression for the potential energy of a dipole of dipole moment p placed in an electric field E. Find the orientation of the dipole when it is in (1) stable equilibrium
(2) unstable equilibrium.
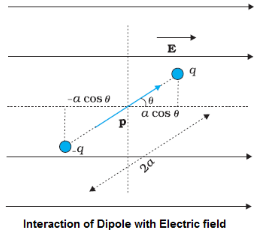
Considera dipole with charges +q and -q placed in a uniform eletric field as shown in figure.
In unifor electric field, dipole experiences a torque τ , which is given by
τ = p×E
where p is electric dipole moment. Torque τ will tend to rotate the dipole if p is not parallel to E .
Suppose an external torque τext is applied to neutalize this torque and rotates the dipole from an angle θ0 to θ1 at an infinitesimal angular speed and without angular acceleration. The amount of workdon by the external torque will be given by W = ![]()
This work is stored as the potential energy of the system.
We can then assosciate potential energy U(θ) with an inclination θ of the dipole. Inorder to choose the reference angular position where potential Energy is considered as zero, we select θo as π/2 as the reference angular position.
We can then write U(θ) = pE( cos(π/2) - cosθ) = -pE cosθ = - p·E
when θ = 0 , i.e., p is aligned in the direction of E, potential energy is minimum.
when θ = π, i.e., p is aligned in the opposite direction of E, potential energy is maximum