derive an expression for the capacitance of a parallel plate capacitor with dielectric medium between the plates, plz provide me a short cut derivation for this question. please help unable to understand such along derivation in refreshers.
Let us take a parallel plate capacitor. Suppose the separation distance between the plates is d. Use air or vacuum as a medium for this experiment.
Suppose +Q is the charge on one plate and �Q is charge on the second plate. Bring a rectangular slab made up of conducting material between the plates of the capacitor. The thickness of the slab must be less than the distance between the plates of the capacitor. When the electric field will be applied then polarization of molecules will be started. The polarization will take place in the direction same as that of electric field. Consider a vector that must be polarized, name it as P. The polarization vector must be in the direction of electric field Eo. Then this vector will start its functioning and will produce an electric field Ep in the opposite direction to that of Eo. The net electric field in the circuit is shown by the figure.
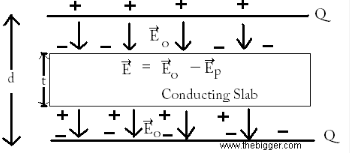
E= Eo � EP
The electric field Eo in the outside region of the dielectric will be null. Now the equation of the potential difference between the plates will be :
V=o (d-t) + Et
But Eo= Er or K
Therefore E= Eo/ k
So
V= Eo (d-t) + Eot / k
V= Eo[d-t+t/k]
As we know
Eo= ![]() /
/ ![]()
= Q / A
![]()
V= Q / A
![]()
Capacitance of the capacitor is shown in the equation below:
C= Q / V= A
![]() / (d-t+t/k)
/ (d-t+t/k)
= ![]()
A /d-t (1-1/K)
I.e. C== ![]()
A/ d-t (1-1/k) ��- 2.31
So, C > Co
Clearly, it is proved that if a dielectric slab is placed in the plates of a capacitor then its capacitance will increase by some amount.