Derive an expression for the apparent frequency when the source of sound is moving towards the listener? (please explain the whole thing…)
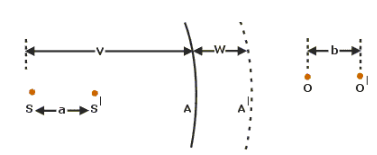
Let S and O denote the initial positions of a source of sound and an observer. For the sake of simplicity, we shall assume that the source, the observer and the medium are all moving along the positive direction.
Let the velocity of sound in still air be = v
The velocity of the source = a
The velocity of the observer = b
and the velocity of the medium (wind blowing) = w
Let Sl and Ol represent the positions of the source and the observer after 1 second. Distance travelled in 1 second is nothing but the velocity.
![]()
The waves produced by the source travel a distance SA in 1 second, but as the wind is blowing with a velocity w, it carries the wavefront from A to Al where A Al= w. The distance travelled by the waves relative to the source in 1 second.
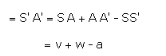
If f is the frequency of the waves produced by the source, then f waves are accommodated in a distance SlAl.
![]()
![]()
Since the observer recedes by a distance b in 1 second, the relative velocity of the waves with respect to the observer is (v + w - b). Therefore, the apparent frequency is given by the number of waves of wavelength ll contained within the above distance.
![]()
Substituting for ll from equation (i), we get
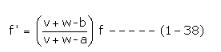
This is the general expression for the apparent frequency of the sound when the source of sound, observer and the medium are in motion, in the same direction.
When source is moving towards the stationary observer:
Let us assume that the wind velocity is zero. Then w = 0 and b = 0. Equation (1-38) becomes
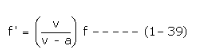
The apparent frequency will be greater than the actual frequency.