Derive an expression for electric intensity due to electric dipole along axial line and equitorial line.
(a) For points on axial line
The axial line of a dipole is the line passing through the positive and negative charges of the electric dipole.
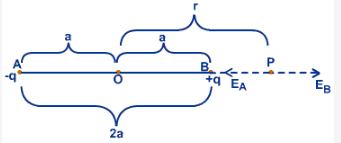
Consider a system of charges (-q and +q) separated by a distance 2a. Let ‘P’ be any point on an axis where the field intensity is to be determined.
Electric field at P (EB) due to +q
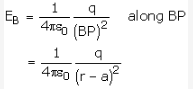
Electric field at P due to -q (EA)
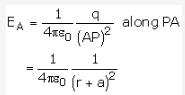
Net field at P is given by
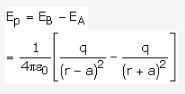
Simplifying, we get

As a special case :
![]()
(b) For points on the equatorial line
An equatorial line of a dipole is the line perpendicular to the axial line and passing through a point mid way between the charges.
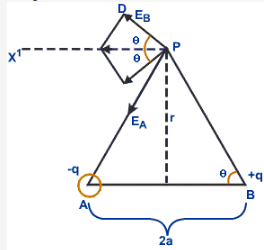
Consider a dipole consisting of -q and +q separated by a distance 2a. Let P be a point Consider a point P on the equatorial line.

The resultant intensity is the vector sum of the intensities along PA and PB. EA and EB can be resolved into vertical and horizontal components. The vertical compents of EA and EB cancel each other as they are equal and oppositely directed. It is the horizontal components which add up to give the resultant field.
![]()
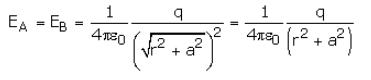
E = 2EA cos q
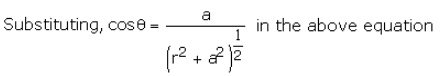
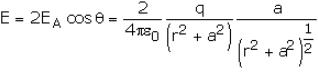
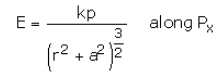
As 2qa = p
As a special case,
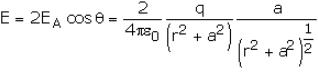
![]()
We find that at very far off points i.e., 2a < r.< r.
Electricity intensity at an axial point is twice the electric intensity on the equatorial line.