Derivation of Young’s Double Slit Experiment and Single slit experiment
Dear student
You are requested to post each query individually.
Young’s double slit experiment:-
Let A and B be two fine slits, a small distance ‘d’ apart. Let them be illuminated by a monochromatic light of wavelength l.
MN in the screen is at a distance D from the slits AB. The waves from A and B superimpose upon each other and an interference pattern is obtained on the screen.
The point C is equidistant from A and B and therefore the path difference between the waves will be zero and so the point C is of maximum intensity. It is called the central maximum.
For another point P at a distance ‘x’ from C, the path difference at P = BP - AP.
Now AB = EF = d, AE = BF = D
\D BPF
[Pythagoras theorem]
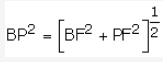
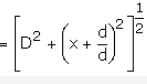
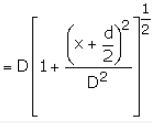
Similarly in D APE
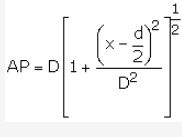
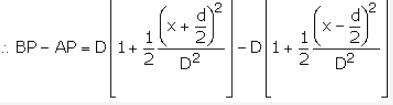
(on expanding Binomially)
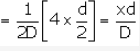
For bright fringes (constructive wavelength) the path difference is integral multiple of wavelength i.e., path difference is nl.
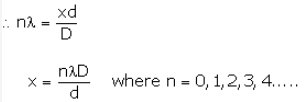
(x therefore represents distance of nth bright fringe from C)
Now
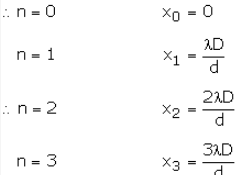
and so on.
![]()
![]()
Therefore separation between the centers of two consecutive bright fringe is the width of a dark fringe.
![]()
Similarly for dark fringes,

The separation between the centers of two consecutive dark interference fringes is the width of a bright fringe.
![]()
All bright and dark fringes are of equal width as b1 = b2.
Note:
The intensity of all bright bands are the same. All dark bands also have same (zero) intensity. The intensity distribution Vs distance is shown as: