Derivation of equations of motion by graphical method

CBSE Class 9
1

Derivation of equations of motion by graphical method

2

First Equation of Motion

Graphical Derivation of First Equation
Consider an object moving with a uniform velocity u in a straight line. Let it be given a uniform acceleration a at time t = 0 when its initial velocity is u. As a result of the acceleration, its velocity increases to v (final velocity) in time t and S is the distance covered by the object in time t.
The figure shows the velocity-time graph of the motion of the object.
Slope of the v - t graph gives the acceleration of the moving object.
Thus, acceleration = slope = AB = image
v - u = at
v = u + at I equation of motion
Graphical Derivation of Second Equation
Distance traveled S = area of the trapezium ABDO
= area of rectangle ACDO + area of DABC
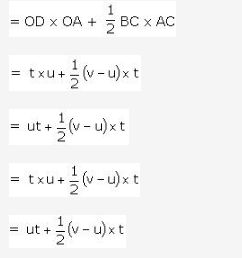
image
(v = u + at I eqn of motion; v - u = at)
image
Graphical Derivation of Third Equation
S = area of the trapezium OABD.
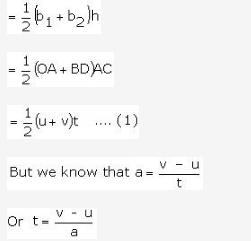
image
Substituting the value of t in equation (1) we get,
2aS = (v + u) (v - u)
(v + u)(v - u) = 2aS [using the identity a2 - b2 = (a+b) (a-b)]
v2 - u2 = 2aS III Equation of Motion