Construct a ∆PQR, in which QR = 6.5 cm, Q = 60° and PR - PQ = 1.5 cm and justify it.
Given, in ∆PQR,
QR = 6.5 cm, ZQ = 60° and
PR - PQ =1.5 cm
Steps of construction
(i)Draw the base, QR = 6.5 cm
![]()
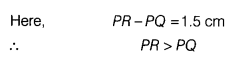
i.e. the side containing the base angle 0 is less than third side, so it is the case II.
(ii)Cut line segment OS equal to PR-PQ, i.e.
OS =1.5 cm from the ray OX extended on opposite side of base QR.
(iii)Join SR and draw its perpendicular bisector ray AB, which intersects SR at M (say).
(iv)Let P be the intersection point of SX and perpendicular bisector AB. Then, join PR.
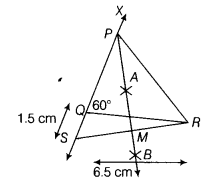
Thus, ∆PQR is the required triangle.
Justification
Base QR and ∠Q are drawn as given.
Since, AB is the perpendicular bisector of SR and P lies on it.
∴ PS = PR
Now, QS = PS - PQ
=> QS= PR-PQ
Thus, construction justified.