Construct a ∆ABC, in which base BC = 3 cm, ∠B = 30° and AB + AC = 5.2 cm. Also justify it.
Given, in ∆ABC, base BC = 3 cm, ∠B = 30° and AB+ AC = 5.2 cm
Steps of construction
(i) First, draw base BC = 3 cm.
(ii) Construct∠YBC = 30° at the point B.
(iii) From ray BY, cut-off line segment BD = AB+ AC = 5.2 cm.
(iv) Join CD.
(v) Draw the perpendicular bisector of CD, which meets BY at A
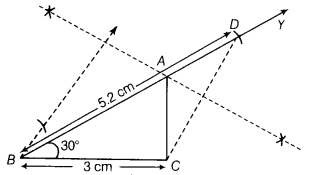
(vi) Join AC. Thus, we get the required ∆ABC.
Justification Since, A lies on the perpendicular bisector of CD.
∴ AC = AD
Now, BD = 5.2 cm =>BA+ AD = 52 cm
∴ BA+ AC = 5.2 cm
.