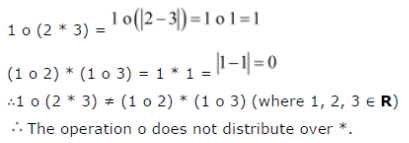Consider the binary operation * : R x R 
R and o = R x R R defined as and R. Show that * is commutative but not associative, o is associative but not commutative. Further, show that R, [If it is so, we say that the operation * distributes over the operation o]. Does o distribute over *? Justify your answer.
