Aim : Finding the refractive index of the prism.
Material required : Prism, piece of white chart of size 20 x 20 cm, pencil, pins,
scale and protractor.
Procedure :
- Take a prism and place it on the white chart in such a way that the triangular base of the prism is on the chart.
- Draw a line around the prism using a pencil. Remove the prism.
- It is a triangle. Name its vertices P, Q and R.
- Find the angle between PQ and PR. This is the angle of the prism (A).
- Mark M on the side of triangle PQ and also draw a perpendicular to the PQ at M.
- Place the centre of the protractor at M and along the normal mark an angle of 30° and then draw line up to M.
- This angle is angle of incidence and note it in a table.
- Place the prism in its position again.
- Now fix two pins vertically on the line at point A and B.
- Look for the images of pins through the prism from the other side and fix another two pins at points C and D in such a way that all the four pins appear to lie along same straight line.
- Now remove the prism and take out pins.
- Draw a line joining the two pin-holes formed by the pins to meet surface PR.
- The angle between the normal at N and the emergent ray is the angle of emergence.
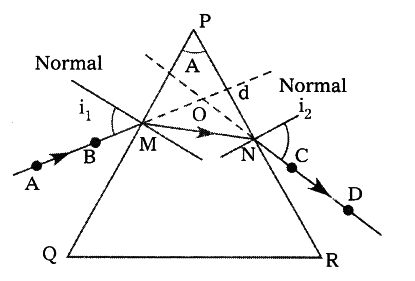
- Join M and N. A, B, M, N, C, D represent the path of light.
- Extend both incident, emergent rays tell they meet at a point ‘O’.
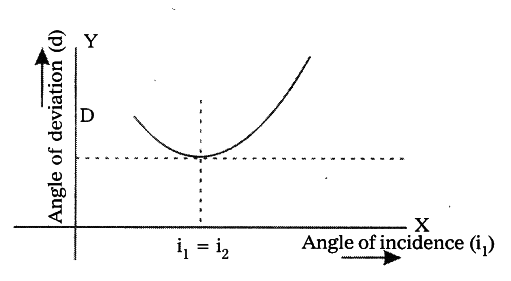
- The angle between these two rays is angle of deviation denoted by ‘D’.
- Do the same for various angles of incidence such as 40°, 50° etc.
- If we take angle of incidence along x-axis and the angle of deviation along y-axis we get the graph as shown in figure.
- The refractive index of prism n = sin[(A + D)/2]/sin A/2