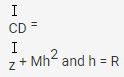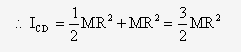Calculate the moment of inertia of a uniform circular disc of radius R and mass M about an axis
a. passing through its center and normal to the disc
b. passing through a point on its edge and normal to the disc.
It is given that moment of inertia of the disc about any of its diameters is
We have, moment of inertia of the disc about its diameter, Id =
![]()
Let us suppose that x and y-axis are the two perpendicular diameters of the disc. Then,
Ix = Iy = Id =![]()
a. If I is moment of inertia of the disc about an axis passing through its centre and normal to its plane, then according to the theorem of perpendicular axis,
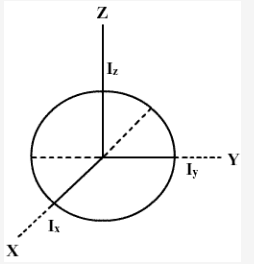
Iz = Ix + Iy =
![]()
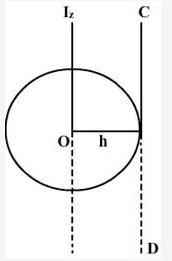
b. If ICD is the moment of inertia of the disc about an axis passing through a point on its edge and normal to its plane, then according to theorem of parallel axis,