Terminal velocity: It is maximum constant velocity acquired by the body while falling freely in a viscous medium.
When a small spherical body falls freely through a viscous medium, three forces act on it.
(i) Weight of the body acting vertically downwards.
(ii) Upward thrust due to buoyancy equal to weight of liquid displaced.
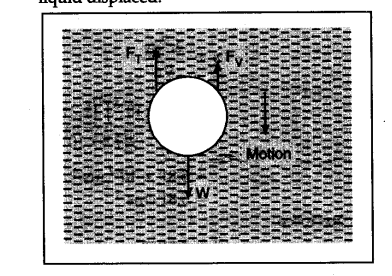
Viscous drag acting in the direction opposite to the motion of body. According to Stoke’s law, FXB, i.e., the opposing viscous drag goes on increasing with the increasing velocity of the body. 1
As the body falls through a medium, its velocity goes on increasing due to ‘gravity. Therefore, the opposing viscous drag which acts upwards also goes on increasing. A stage reaches when the true weight of the body is just equal to the sum of the upward thrust due to buoyancy and the upward viscous drag. At this stage, there is no net force to accelerate the body. Hence it starts falling with a constant velocity, which is called terminal velocity. Let p be the density of the material of the spherical body of radius r and p0 be the density of the medium.
True weight of the body,

It depends upon the terminal velocity varies directly as the square of the radius of the body and inversely as the coefficient of viscosity of the medium. It also depends upon densities of the body and the medium.
Hi there, which book is this - the image you attached?