ABCD is a rectangle and P,Q,R ans S are mid-points of the sides AB, BC, CD and DA, respectively. Show that the quadrilateral PQRS is a rhombus.
Given, ABCD is a rectangle.
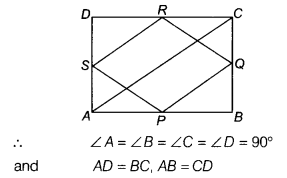
Also, given P, Q, R and S are the mid-points of
AB, SC, CD and DA, respectively.

Thus, PQ=SR . …(i)
Now, in ∆ASP and ∆ BQP
AP = BP [∵ P is the mid-point of AB]
AS = BQ

From Eqs. (i), (ii) and (iii), it is clear that quadrilateral
PQRS is a rhombus