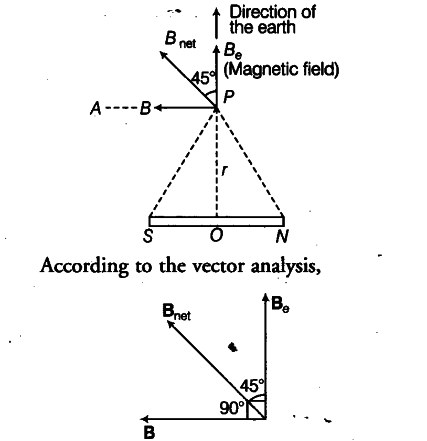
A short bar magnet of magnetic moment 5.25 x ${{10}^{-2}}$ J/T is placed with its axis perpendicular to the earth’s field direction. At what distance from the centre of the magnet, the resultant field is inclined at 45° with the earth’s field on (i) its normal bisector and (ii) its axis. Magnitude of the earth’s field at the place is given to be 0.42 G. Ignore the length of the magnet in comparison to the distances involved.
Given, magnetic moment, m = 5.25 X {{10}^{-2}} J/T
Let the resultant magnetic field be { B }_{ net }
It makes an 45° angle with { B }_{ e }
{ B }_{ e } = 0.42 G = 0.42 x {{10}^{-4}} T
(i) At Normal Bisector
Let r be the distance between axial line and point P. The magnetic field at point P, due to a short magnet,
B = { µ }_{ 0 } / 4v$\pi$ . m / {{r}^{3}}
The direction of B is along PA, i.e. along TV-pole to 5-pole.
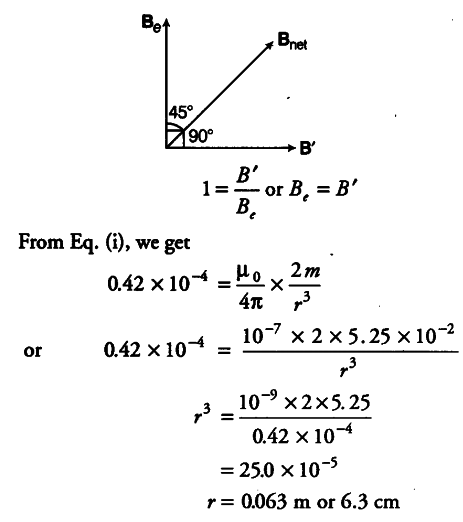
tan 45° = B sin 90° / B cos 90° + { B }_{ e }
1 = B / { B }_{ e }
We get ,
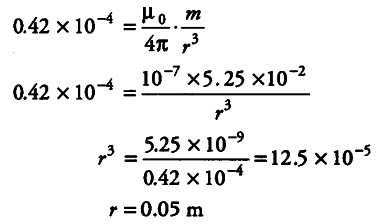
(ii) When Point Lies on Axial Line
Let the resultant magnetic field Baa makes an angle 45 ° from Be. The magnetic field on the axial line of the magnet at a distance of r from the centre of magnet.
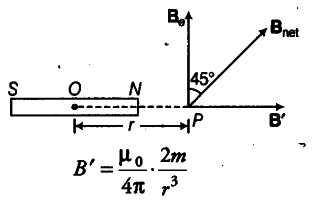
Direction of magnetic field is from 5 to N. According to the vector analysis.
tan 45 ° = B’ sin 90° / B’ cos 90° + { B }_{ e }