An insulating sphere of radius a, centered at the origin, has a uniform volume charge density ?.
Find the electric field E? (r? ) inside the sphere (for r< a) in terms of the position vector r?.
Express your answer in terms of r?,? (Greek letter rho), and ?0
Concepts and reason
Use the concept of Gauss law in electrostatics to solve this problem.
The electric field intensity of the sphere can be calculated by using the Gauss law for electrostatics.
The charge enclosed inside the sphere can be calculated by using the relation between the charge enclosed, volume, and density.
The required electric field intensity can be calculated using the value of charge in the expression of electric field intensity.
Fundamentals
The Gauss’s law states that the net flux out of a closed surface is equal to the charge enclosed inside the body by the permittivity. It is expressed as follows:
Answer:
Calculate the electric field intensity.
The Gauss’s law is expressed as follows:
![]()
![]()
![]()
Explanation:

Calculate the charge enclosed inside the sphere.
The expression to calculate the charge enclosed in a surface is,
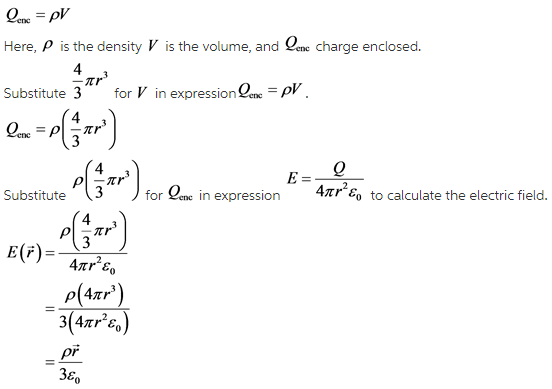
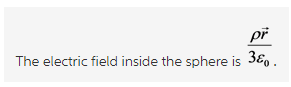
Explanation:
The electric field inside the sphere varies linearly and is directly proportional to the radius.
