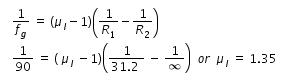An eqviconvex lens incontact with liquid layer on top of plane mirror. a small pin with its tip on the principle axis is moved alone the axis till its vertical image is formed at the position of niddle distance of niddle from lens is 45cm. and now liquid is removed and experiment is repeated now new distance between niddle and lens id 30cm then what is refractive index
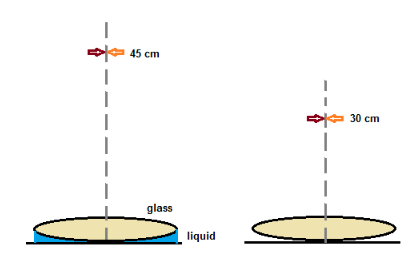
As shown in figure, focal length of lens is found as 45 cm with liquid layer below the lens.
This is considered as combination two lens, one equi-convex lens made of glass and other one plano-concave lens made of liquid.
In another experiment, convex lens alone is used to get the focal length 30 cm.
Let F be the focal length of lens combination, fg is the focal length of glass lens and fl is the focal length of liquid lens.
we have, 1/F = ( 1/ fl ) + ( 1 / fg ) , hence 1/45 = ( 1/ fl ) - ( 1 / 30 ), hence we get fl = 90 cm
( focal length of plano-concave lens is negative).
using lens maker’s formula, refractive index of glass and measured focal legth we get radius of crvature of glass lens as given below
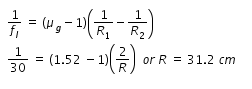
where R1 and R2 are radii of curvature of glass lens. It is considered that they are equal and the equal radius of curvature is found as above.
For the lens combination, radius curvature of concave lens (liquid lens) is same as the radius of curvature of glass lens.
In the liquid lens one side is plane, hence radius of curvature of planar side is infinity.
Now using again lens makers formula for liquid lens, focal length and radius of curvature we find refractive index of liquid μl as follows.