An aeroplane can carry a maximum of 200 passengers. A profit of Rs. 1000 is made on each executive class ticket and a profit of Rs. 600 is made on each economy class ticket. The airline reserves at least 20 seats for executive class. However, at least 4 times as many passengers prefer to travel by economy class than by the executive class. Determine how many tickets of each type must be sold in order to maximize the profit for the airline. What is the maximum profit?
Let x be the number of executive class tickets and y be the number of economy class tickets sold by the airline, respectively.
Profit on each executive class ticket = Rs. 1000
Profit on x executive class tickets = Rs. 1000x
Profit on each economy class tickets = Rs. 600
Profit on y economy class tickets = Rs. 600y
Therefore, total profit = Rs. (1000x + 600y)
Let Z denote the total profit, then
Z = 1000 x + 600 y
As the aeroplane can carry a maximum of 200 passengers, therefore
![]()
Since at least 20 executive class tickets are reserved, therefore
x > 20
Since the number of tickets cannot negative, therefore
![]()
So, the mathematical formation of given LPP is as follows:
Maximize Z = 1000 x + 600 y …(1)
Subject to the constraints
![]() …(2)
…(2)
x![greater or equal than]
x≥20 …(3)
y≥4x
We draw the lines
x + y = 200, x = 20 and y = 4x.
on suitable scale in the 1st quadrant.
Corner point method : The corner points of the feasible region (shaded) ABC are
A(20, 80), B (40, 160) and C (20, 180)
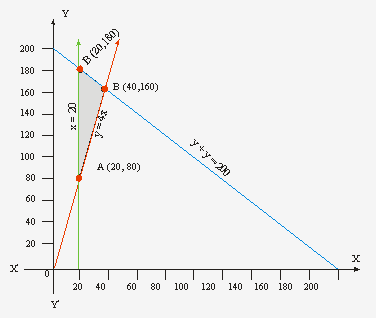
Note that the coordinates of A, B and C are obtained by solving x = 20, y = 4x; y = 4x and x+ y = 200; x = 20 and x + y = 200.
The value of the objective function Z at these points are given in the following table:

From the table, we see that the maximum value of Z is 136000 at the point (40, 160).
Thus, x = 40, y = 160 is the optimal of the given LPP. Hence, the airline should sell 40 executive class tickets and 160 economy class tickets to maximize profit. The maximum profit is Rs. 1,36,000.