ABCD is a cyclic quadrilateral, whose diagonals intersect at a point E. If ∠DBC = 80° and ∠BAC = 40°, then find ∠BCD. Further, if AB = BC, then find ∠ECD.
Given, in quadrilateral, ∠BAC = 40°
and ∠DBC = 80°
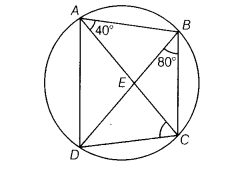
here, ∠CDB= ∠BAC= 40°
[∴ angles in the same segment of a circle are equal]
In ∆BCD, ∠DBC + ∠BCD + ∠CDB = 180°
[ ∴ sum of all angles of a triangle is 180° ]
80° + ∠BCD + 40° = 180° [from Eq. (i)]
∠BCD = 180° -40° - 80°
∠BCD = 60° …(ii)
In AABC, AB = BC [given][ ∴
[ ∴angles opposite to equal sides of a triangle are equal]
∠BCA = 40° [from Eq. (i)] …(iii)
From Eq. (ii), we have ∠ BCD = 60°
∠BCA + ∠ACD = 60°
40° + ∠ACD = 60° [from Eq. (iii)]
∴ ∠ACD = 20° or ∠ECD = 20°