∆ABC is an isosceles triangle in which AB = AC. D, E and F are the mid-points of the sides BC, AC and AB, respectively. Prove that DE = DF.
Given In ∆ABC, AB = AC and D, E and P are the mid-points of the sides BC, AC and AB, respectively.
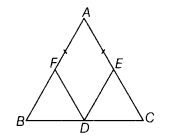
To prove DE = DF
Proof In ∆ABC, we have
AB=AC
1/2AB=1/2AC
BF=CE
∠C = ∠B …(ii)
[∵ AB = AC and angles opposite to equal sides are equal]
Now, in ∆ BDF and ∆ CDE, DB = DC
[∵ D is the mid-point of BC]
BF = CE [from Eq. (i)]
and ∠C = ∠B [from Eq. (ii)]
![]()
Hence, DF = DE