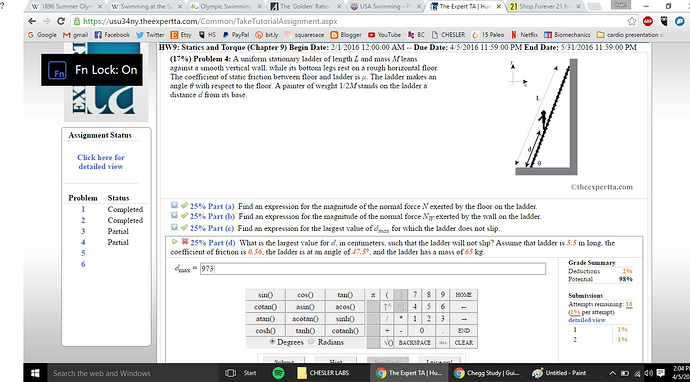
A uniform stationary ladder of Length L and mass M leans against a smooth vertical wall,while its bottom legs rest on a rough horizontal floor. The coefficient of static friction between the floor and ladder is miu. The ladder makes an angle theta with respect to the floor. A painter of weight 1/2M stands on the ladder a distance d from its base.
Answer:
“smooth vertical wall” means there is no friction there, so the only vertical forces are the weights of the ladder and painter and the normal force at the floor.
a) “Find an expression for the magnitude of the normal force, N, exerted by the floor on the ladder.”
As stated above, we know that
N = (M + ½M)g = 3Mg / 2
b) “Find an expression for the magnitude of the normal force, Nw, exerted by the wall on the ladder.”
Sum the moments about the base of the ladder:
ΣM = 0 = MgL/2cosΘ + ½MgdcosΘ - NwLsinΘ
0 = ½MgcosΘ*(L + d) - NwLsinΘ
Nw = Mg(L+d) / 2LtanΘ = Mg(1 + d/L) / 2tanΘ
c) “Find an expression of the largest value of d-max for which the ladder does not slip.”
Since they are the only two horizontal forces in play, we know that
Nw = Ff where Ff is the friction force at the floor, and Ff = µN = µ3Mg / 2. So
Mg(L+d) / 2LtanΘ = µ3Mg / 2 → Mg/2 cancels
(L+d) / LtanΘ = µ3
L+d = 3µLtanΘ
max d = L(3µtanΘ - 1)
d) “What is the largest value for d, in cm, such that the ladder will not slip?”
max d = 5.5m * (30.56tan47.5º - 1) = 4.58 m = 458 cm