A triangle ABC is drawn to circumscribing a circle of radius 3cm such that segments BD and DC into BC is divided by the point of contact D are of length 9cm. And 3 cm. Respectively. Find the sides AB and AC.
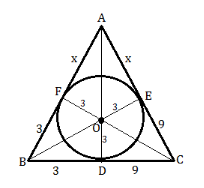
Consider the above figure. We assume that the circle touches AB in F, BC in D and AC in E. Also given is BD = 9cm and DC = 3cm.Let AF = x.
For ΔABC, AF = AE = x (∵ tangents drawn from an external point to a circle are congruent i.e. AE and AF are tangent drawn from external point A.)
Similarly, we have, BE = BD = 3 cm (∵ congruent tangents from point B)
And CF = CD = 9 cm (∵ congruent tangents from point C)
Now, AB = AE + EB = x + 3
BC = BD + DC = 12
AC = AF + FC = x + 9
Then,
2s = AB + BC +CA = x + 3 + 12 + 1 + x + 9 = 2x + 24
∴ s = x + 12
Using Heron’s formula,

