A spherical conducting shell of inner radius ${ r }{ 1 }$ and
outer radius ${ r }{ 2 }$ has a charge Q.
(i) A charge q is placed at the centre of the shell. What is the surface charge density on the inner and outer shells?
(ii) Is the electric field inside a cavity (with no charge) zero, even if the shell is not spherical but has any irregular shape? Explain.
(i) The charge + Q resides on the outer surface of the shell. As the charge q is placed at the centre of the shell, there is charge - q induced on the inner surface and a charge + q is induced on the outer surface of the shell. Thus, the total charge on the inner surface of the shell is — q and on the outer surface of the shell is (Q + q).
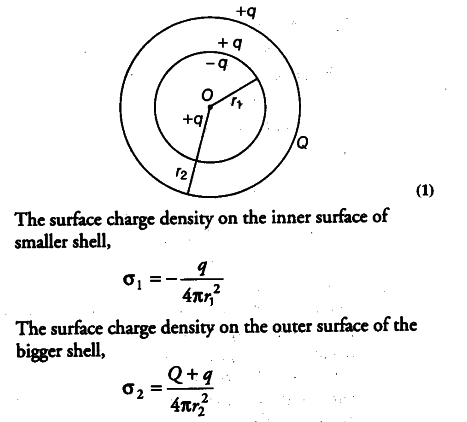
(ii) Yes, the electric field inside a cavity is zero, if the shape of the shell is not spherical, If we take a closed loop which is inside the cavity along a field line and the rest outside it, the net work done by the field in carrying a test charge over the closed loop will not be - zero. So, the electric field inside a cavity with no charge is always zero.