A regulation table tennis ball has a mass of 2.7g and is 40mm in diameter. What is its moment of inertia about an axis that passes through its center?
Concepts and reason
The concepts required to solve this problem are moment of inertia of the hollow sphere and conversion of units.
First solve for the radius of the sphere from diameter and convert mass to kilogram. Then, substitute the values in the expression of moment of inertia of hollow sphere to calculate the moment of inertia of the tennis ball about an axis that passes through its center.
Fundamentals
The radius of a sphere is half of the diameter. That is,
Here, r is the radius and d is the diameter.
The moment of inertia of hollow sphere about an axis that passes through its center is,
Here, I is the moment of inertia, m is the mass, and r is the radius.
The relations used to coverts units are as follows:
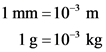
Answer:
The relation of diameter and radius is.
Explanation:
The radius is half of the diameter of the tennis ball.
The expression of moment of inertia of the tennis ball is,
Substitute 
for m, and 
in the equation and calculate the moment of inertia of the tennis ball about an axis that passes through its center.
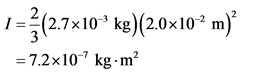
The moment of inertia of the tennis ball about an axis that passes through its center is 
.
Explanation:
The tennis ball is made of a plastic cover with hollow inside. The hollow sphere is the closest symmetry of the tennis ball.