A metallic rod of length ‘L’ is rotated with angular frequency of ‘L’ with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius R, about an axis passing through the centre and perpendicular to the plane of the ring. A constant and uniform magnetic field B parallel to the axis is present everywhere. Deduce the expression for the emf between the centre and the metallic ring.
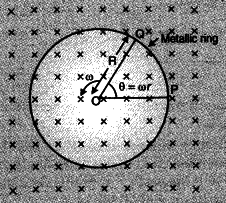
The magnitude of the emf, generated across a length dr of the rod, as it moves at right angles to the magnetic field, is given by d\varepsilon =Bvdr
Therefore,
\[\varepsilon =\oint{d\varepsilon =\int_{0}^{R}{Bvdr=\int\limits_{0}^{R}{B\omega rdr=\frac{B\omega \mathop{R}^{2}}{2}}}}\]