(a) A magnetic dipole is placed in a uniform magnetic field with its axis tilted with respect to its position of stable equilibrium. Deduce an expression for the time period of (small amplitude) oscillation of this magnetic dipole about an axis, passing through its centre and perpendicular to its plane.
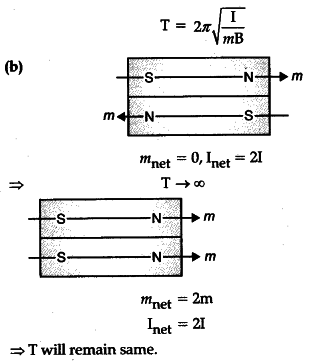
(b) If this bar magnet is replaced by a combination of two similar bar magnets, placed over each other, how will the time period vary ?
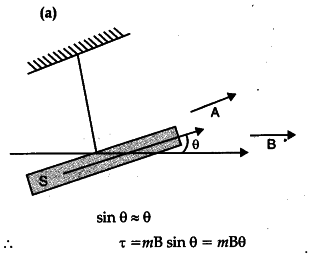
This torque is in the nature of a restoring torque.
Hence, the equation of motion, for the oscillatory motion, of the magnet is
I\frac { { { d }^{ 2 } }\theta }{ d{ t }^{ 2 } } =-mB\theta
This is the equation of a S.H.M.
\frac { { { d }^{ 2 } }\theta }{ d{ t }^{ 2 } } +{ w }^{ 2 }\theta =0
Where { \omega }^{ 2 }=\frac { mB }{ I }
Hence the time period of oscillation of the magnet is given by
T=\frac { 2\pi }{ \omega }