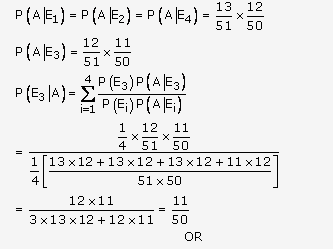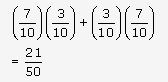A card form a pack of 52 cards is lost. From the remaining cards of the pack, two cards are drawn at random and are found to be both clubs. Find the probability of the lost card being of clubs.
OR
From a lot of 10 bulbs, which includes 3 defectives, a sample of 2 bulbs is drawn at random. Find the probability distribution of the number of defective bulbs.
Let the events E1 E2 E3, E4 and A be defined as follows:
E1: Missing card is a diamond
E2: Missing card is a spade
E3: Missing card is a club
E4: Missing card is a heart
A: Drawing two club cards
P(E1) = P( E2) = P( E3)=P( E4) =1/4
Total number of bulbs = 10
Number of defective bulbs = 3
Number of non defective bulbs = 7
P(drawing a defective bulb) ,p =3/10
P(drawing a non defective bulb),q =7/10
Two bulbs are drawn let X denotes the number of defective bulbs then X can take values 0, 1, 2
P(X = 0) = P(drawing both non defective bulbs) =(7/10)2
P(X = 1) = P(drawing one defective and one non defective bulb)
= P (drawing a non defective bulb and a defective bulb) + P (drawing a
defective bulb and a non defective bulb)
=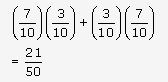
P(X = 2) = P(drawing both defective bulbs)=(3/10)2
Required Probability distribution is