An AC voltage V = ${ V }_{ m }$ sin ωt is applied across an inductor of inductance L. Find the instantaneous power Pi supplied to the inductor. Show graphically the variation of Pi with ωt.
In an inductor, the current lags the voltage by 90°. If the source voltage is sinusoidal, then the current is also sinusoidal, but shifted in phase. The instantaneous power defined as the product of the instantaneous voltage and current can also be seen to be sinusoidal in time. However, in contrast to the resistive load, the instantaneous power in the inductor goes negative for part of the cycle of the source driving it.
As , V(t) = { V }_{ m } sin ωt
I(t) = - { I }_{ m } cos ωt
Instantaneous velocity = V(t). I(t)
= { V }_{ m } sin ωt x
-
{ I }_{ m } cos ωt
=- { V }_{ m } Im/ 2 [ sin2 ωt + sin-0] -
{ V }_{ m } Im/2 sin 2 ωt
The variation of { P }_{ i } with ωt is as given in the figure.
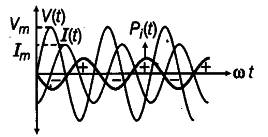
The instantaneous power alternates positive_and negative at twice the frequency of source supplying it.