An oscillator creates periodic waves on a stretchedstring.
If the period of the oscillator doubles, whathappens to the wavelength and wave speed?
If the amplitude of the oscillator doubles,what happens to the wavelength and wave speed?
Concepts and reason
The concepts used to solve this problem are wavelength of the wave and wave speed in string.
Wavelength of the wave is the distance between two successive points on a wave that are in the same state of oscillation.
Use the expression of wavelength of wave in terms of speed and frequency of the wave to find the dependence of period on wavelength of the wave.
Wave speed is the speed in which wave can travel.
Use the expression of wave speed on a string to find the dependence of period on wave speed.
Fundamentals
The expression of wavelength of wave in terms of speed and frequency of the wave is,
Here,f is the frequency of the wave, 
is the wavelength of the wave, and v is the speed.
Expression for the frequency of the wave is ,
Here, T is the period of the wave.
Expression for the wave speed in string is,
Here, v is the wave speed in string, t is string tension, m is string mass, and L is string length.
Answer:
Here, t is the tension in the string.
The speed of the wave does not depend on the period of the wave. Hence, the wave speed remains unchanged when the period of the oscillator doubles.
Therefore, the correct option is the wavelength doubles but the wave speed is unchanged if the period of the oscillator doubles.
Part 1
The wavelength doubles but the wave speed is unchanged.
(2)
The expression of wavelength of wave in terms of speed and frequency of the wave is,
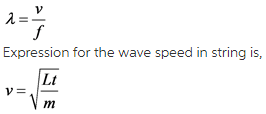
Here, t is the tension in the string.
The wavelength and speed of the wave do not depend on the amplitude of the oscillator. Therefore, both the wavelength and wave speed are unchanged if the amplitude of the oscillator doubles
Part 2
Both the wavelength and wave speed are unchanged.