Answer the following questions regarding the earth’s magnetism:
(i) A vector needs three quantities for its specification. Name the three independent quantities conventionally used to specify the earth’s magnetic field.
(ii) The angle of dip at a location in Southern India is about 18°. Would you expect a greater or smaller dip angle in Britain?
(iii) If you made a map of magnetic field lines at Melbourne in Australia, would the lines seem to go into the ground or come out of the ground?
(iv) In which direction would a compass free to move in the vertical plane point to, if located right on the geomagnetic North or South pole?
(v) The earth’s field, it is claimed, roughly approximates the field due to a dipole of magnetic moment 8 x ${{10}^{22}}$ J/T located at its centre. Check the order of magnitude of this number in some way.
(vi) Geologists claim that besides the main
magnetic N-S poles, there are several local poles on the earth’s surface oriented in different directions. How is such a thing possible at all?
(i) The three independent quantities required to specify the earth’s magnetic field are as follows: Magnetic declination, angle of dip and horizontal component of earth’s magnetic field, they are called the magnetic elements of the earth.
(ii) We can expect a greater value of angle of dip in Britain because Britain is located close to North pole. The value of angle of dip in Britain is about 70°.
(iii) Melbourne is situated in Southern hemisphere and at Southern hemisphere, the North pole of earth’s magnetic field lies. So, the magnetic field lines seem to come out of the ground as magnetic field lines emerge from North pole and enter in South pole.
(iv) As we know that, at the poles, the earth’s magnetic
field is exactly vertical. The compass needle is always free to rotate in horizontal plane only, so at the poles it may point out in any direction.
(v) Magnetic moment of dipole , M = 8 x {{10}^{22}} J/T
Now, we calculate the magnetic field intensity at magnetic equator of the earth. We consider that at a point on equatorial line of short magnetic dipole for which distance d= R (radius of the earth).
Radius of the earth, R = 6400 km =6.4x${{10}^{6}}$m
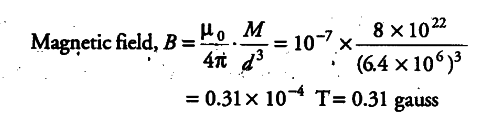
(vi) The earth’s magnetic field is only due to the dipole field. As there are several local N-S poles that may exist oriented in different directions, so they may nullify the effect of each other. These local N-S poles may occur due to the deposition of magnetised minerals.