The parking charges of a car in a parking lot is ₹ 30 for the first two hours and ₹10 per hour for subsequent hours. Taking total parking time to be x h and total charges as ₹y, write a linear equation in two variables to express the above statement. Draw a graph for the linear equation and read the charges for five hours.
Given, parking charges for the first two hours = ₹30
and for subsequent hours = ₹ 10
Total parking time = xh and total charges = ₹y
Then, according to the given condition,
30 + 10(x-2) = y=> 30 + 10x -20 = y
=>10x + 10-y = 0
=>10x-y+10 = 0 (i)
which is the required linear equation in two variables.
It can also be written as
y = 10x + 10 ,…(i)
Now, for drawing the graph, we need atleast two solutions of the equation.
When x = 0, then y = 10(0) +10 = 10
When x = -1, then y = -10 + 10 = 0
When x = 1, then y = 10(1) + 10 = 20
So, we have the following table to draw the graph

Here, we have three points A(-1, 0), B (0,10) and C(1,20). By plotting these points on the graph paper and joining them, we get a straight line AC, which represents the required graph of linear equation.
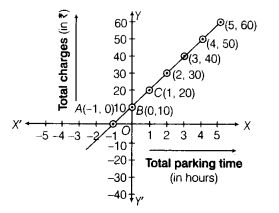
From the graph, charges for the hours 1,2, 3, 4 and 5 are ₹ 20, ₹ 30,₹ 40, ₹ 50 and ₹ 60, respectively.