Prove that the difference between any two sides of a triangle is less than its third side.
Let us consider a ∆ABC, whose sides are AB, BC and CA.
To prove AC - AB < BC, BC - AC < AB and BC - AB < AC
Construction Let AC > AB. Then, along AC, cut-off AD = AB and join BD.
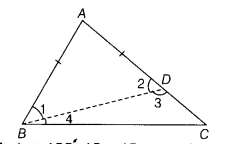
Proof In ∆ ABD, AB=AD⇒ ∠2=∠1
[∵ angles opposite to equal sides are equal]
Side CD of ∆ BCD has been produced to A.
∠2 >∠4
[∵ exterior angle is greater than each interior opposite angle]
Again, side AD of ∆ABD has been produced to C.
∴∠3>∠1 …(iii)
[∵ exterior angle is greater than each interior opposite angle]
From Eqs. (i) and (iii), we get∠3 > ∠2
Now, ∠3 >∠2 and ∠2 > ∠4 => ∠3 > ∠4
∴BC >CD
[∵ sides opposite to greater angle is longer]
⇒ CD < BC ⇒ AC - AD < BC
Hence, AC - AB < BC [∵ AD = AB]
Similarly, BC - AC < AB and
BC - AB< AC Hence proved.