Prove that, lines which are parallel to the same line, are parallel to each other.
Given Three lines a, b and c such that a||c and b||c.
To prove a||b
Construction Draw a transversal r cutting a, b and c at points P, Q and R, respectively.
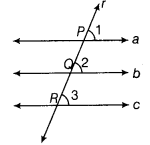
Proof Since, parallel lines a and c are intersected by the transversal r at points P and R, respectively.
∴∠1 = ∠3 [corresponding angles axiom] …(i)
Again, parallel lines b and c are intersected by the transversal r at points Q and R , respectively.
∴ ∠2 = ∠3 [corresponding angles axiom] …(ii)
From Eqs. (i) and (ii), we get ∠1 = ∠2
But these are corresponding angles.
∴ a||b [by converse of corresponding angles axiom]