In the given figure, prove that CD + DA + AB + BC > 2 AC.
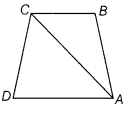
In ∆ABC, the sum of two sides of a trangle is greater than the third side,
∴AB + BC > AC …(i) (1)
In ∆ACD, the sum of two sides of a triangle is greater than the third side,
∴CD + DA > AC . …(ii) (1)
On adding Eqs. (i) and (ii), we get
CD + DA+ AB + BC > 2AC.