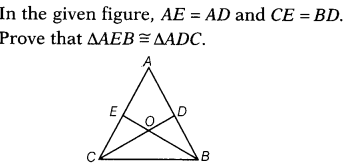
Given, AE = AD
and CE = BD
On adding Eqs. (i) and (ii), we get
AE + CE = AD + BD
=> AC = AB
Now, in ∆AEB and ∆ADC, we have
AE = AD [given]
AB = AC [proved above]
and ∠A = ∠A [common angle]
∴ ∆AEB =∆ADC [by SAS congruence rule]

Given, AE = AD
and CE = BD
On adding Eqs. (i) and (ii), we get
AE + CE = AD + BD
=> AC = AB
Now, in ∆AEB and ∆ADC, we have
AE = AD [given]
AB = AC [proved above]
and ∠A = ∠A [common angle]
∴ ∆AEB =∆ADC [by SAS congruence rule]