In the given figure, A and B are the end points of a diameter of a circle with centres at P and C is a point on the circumference of the circle such that ∠ABC = 35°, then find the value of ∠ACP.
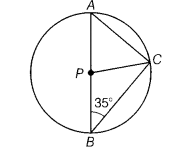
In ∆PBC,PC = PB [radii of the circle]
=> ∠PBC = ∠PCB = 35°
[∵ angles opposite to equal sides of a triangle are equal]
Also, ∠ACB = 90°
[∵ angle in semi-circle is 90°]
=> ∠ACP +∠PCB = 90°
=> ∠ACP = 90° - 35°= 55°